Colpitts Oscillator

The SFG of a third-order oscillator is shown in Fig.1.α. The implementation of this SFG could be done by using the topology in Fig.1.β. This is a feedback loop that consists of a current amplifier-inverter (180^o phase shift), and a third-order lowpass LC network for introducing an additional phase shift of 180^o in order the total phase shift in the loop to be equal to zero.

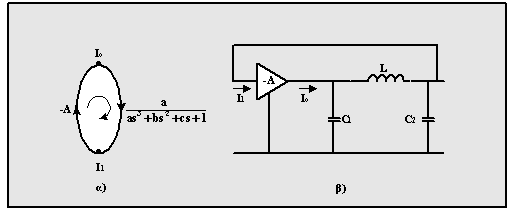
Fig.1 α) SFG of a third-order oscillator

β) Implementation of the SFG in Fig.1a

The loop gain of the circuit in Fig.1.β is given by

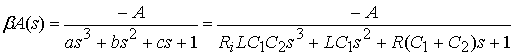
According to the above expression, we can calculate the phase of the loop as,

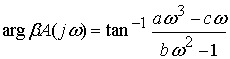
The phase become equal to zero at a specific frequency ω_o

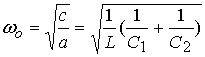
which is the oscillation frequency.

The loop gain will be become equal to one if the following condition is fulfilled

This relationship describes the condition of oscillation.

In the topology of Fig.1β capacitors can be replaced by inductors and the inductor can be replaced by a capacitor to create a highpass third order LC network. This topology is the well-known Hartley oscillator.

A real circuit of a Colpitts oscillator, using a BJT as an active element, is shown in Fig.2; note that in this case A=h_fe.

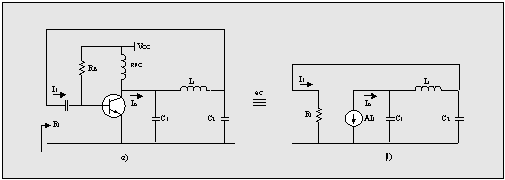
Fig.2 α) Colpitts oscillator realized using a BJT transistor

β) Small-signal eqivalent of the circuit in Fig.2a

Colpitts oscillators are suitable for operation at radio frequencies.

Design example

Using a BJT with h_fe=100, we will design a Colpitts oscillator at f_o =2 MHz.

According to the condition of oscillation

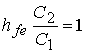
or,

The frequency of oscillation is defined by,

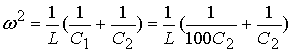
or,

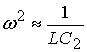
Choosing,

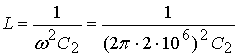
and C₂=3.2 nF it results, C₁=320 nF and L=1,97 μH.